Block-Diagonal-Newton-Raphson-Methode
Bei dieser Methode wird die  Hesse-Matrix
in einzelne 3x3-Matrizen für jedes Atom unterteilt (geht nur in
Hesse-Matrix
in einzelne 3x3-Matrizen für jedes Atom unterteilt (geht nur in  kartesischen
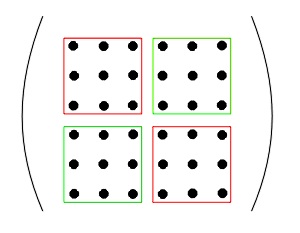
Koordinaten). Die 3x3-Matrizen entlang der Diagonale (rot) werden zur
Berechnung der nächsten Iterationskoordinaten benutzt, die außerhalb
der Diagonale (grün) werden vernachlässigt.
kartesischen
Koordinaten). Die 3x3-Matrizen entlang der Diagonale (rot) werden zur
Berechnung der nächsten Iterationskoordinaten benutzt, die außerhalb
der Diagonale (grün) werden vernachlässigt.
Damit verkürzt man die Rechenzeit,
da man nicht die gesamte Hesse-Matrix, sondern nur die 3x3-Matrizen berechnen
und invertieren muß. Die einzelnen Iterationsschritte werden damit
schneller, aber die Genauigkeit sinkt.
Wie bei der steepest-descent-Methode nimmt
die Schnelligkeit der Konvergenz in der Nähe des Minimums ab.
Deshalb ist in einigen Programmen eine
Kombination aus der Block-Diagonal- oder steepest-descent- (weiter entfernt
vom Minimum) und der Newton-Raphson-Methode (in der Nähe des Minimums)
integriert.
 Hesse-Matrix
in einzelne 3x3-Matrizen für jedes Atom unterteilt (geht nur in
Hesse-Matrix
in einzelne 3x3-Matrizen für jedes Atom unterteilt (geht nur in  kartesischen
Koordinaten). Die 3x3-Matrizen entlang der Diagonale (rot) werden zur
Berechnung der nächsten Iterationskoordinaten benutzt, die außerhalb
der Diagonale (grün) werden vernachlässigt.
kartesischen
Koordinaten). Die 3x3-Matrizen entlang der Diagonale (rot) werden zur
Berechnung der nächsten Iterationskoordinaten benutzt, die außerhalb
der Diagonale (grün) werden vernachlässigt.