Wenn man die Molekülorbital-Ausdehnungskoeffizienten c_mi aus der  LCAO-Methode bestimmt hat, dann kann man über die  Slater-Determinante die Gesamtwellenfunktion des Systems berechnen. Mit der Schrödinger-Gleichung erhält man die Energie des Systems.

Um die Koeffizienten zu bestimmen, macht man sich das Variationsprinzip zunutze, das besagt, daß für den Grundzustand jeder antisymmetrischen,  normierten Funktion der Elektronen-Koordinaten (genannt X) der Energiewert größer ist als für die tatsächliche exakte Wellenfunktion Y.

 (15)

Daraus ergibt sich, daß die Energie der exakten Wellenfunktion E(Y) eine untere Schranke der Energien ist, die sich aus allen anderen normierten, antisymmetrischen Wellenfunktionen ergeben. Damit kann man die Koeffizientenmenge bestimmen, die als Resultat beim Einsetzen in die Schrödinger-Gleichung die exakte Energie liefert.

Man leitet die  Integralgleichung für die Energie, die sich durch Umformen aus der Schrödinger-Gleichung ergibt, nach den Koeffizienten ab und setzt die Ausdrücke, die sich daraus ergeben, gleich Null.

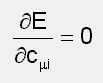 (16)